Расчет неопределенности

Расчет неопределенности результата измерения
В реальных условиях практически невозможно добиться абсолютно точных измерений, т. к. множество факторов вносит свои коррективы. Отсюда возникает потребность ввести такой параметр, который будет характеризовать отклонения, от реального значения измеряемой величины.
Так в 1993 г. в метрологию был введен термин «неопределенность», в связи с выходом ISO IEC «Руководство по выражению неопределенности измерений», в котором и была размещена трактовка данного термина.
Неопределенность измерения – параметр, который связан с результатом измерения и характеризующий разброс значений, которые могли бы быть приписаны измеряемой величине.
Причины появления неопределенностей:
- Субъективность оператора,
- Разрешающая способность СИ,
- Несовершенный метод измерения,
- Неполное описание измеряемой величины,
- Использование при обработке данных неточных значений констант и других параметров .
Выделяются следующие виды неопределенностей:
- Стандартная неопределенность,
- Суммарная стандартная неопределенность,
- Расширенная неопределенность.
В соответствии с использованием оценки числовых значений составляющих НРИ они разделяются на два типа А и В. Оценки неопределенности по типу А получены на основании обработки ряда экспериментальных данных, а оценки неопределенности по типу В на основании дополнительной информации полученной из любых других источников (как пример: из свидетельства о поверки).
Составляющие типа А оцениваются путем статистического анализа результатов измерения и будут характеризоваться экспериментальным СКО.
Составляющие типа В оцениваются любым другим способом кроме статистических, т. К. используется информация основанная на базе научного суждения.
На начальном этапе составляется математическая модель измерения
В основном измеряемая величина Y не является прямоизмеряемой, а зависит от входных величин x1, x2,… участвующих также в процессе измерения. Поэтому выходной оценкой Y является следующая зависимость : Y = f (x1, x2,…. xn), которая и является результатом измерения.
В прямом измерении входная величина совпадает с выходной, потому учитывая поправки ее можно представить в виде : X = Xi+1+&1+&2, где Xi – окончательный результат измерения согласно методике измерения (для многократных измерений – среднее арифметическое полученных значений, для однократного – показание прибора)
&1,2 – поправки (как пример: поправка на погрешность СИ, поправка на вариационный разброс измерения, поправка влияния окружающей среды)
Для составления точной математической модели важно знать и учитывать физический принцип измерения, а в некоторых случаях и устройство и принцип работы СИ с помощью которого был получен результат.
Этап анализа входной величины и неопределенностей
Стандартная неопределенность по типу А – это результаты многократных измерений, на основании которых рассчитывается среднее арифметическое:
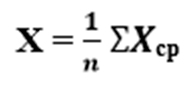
После чего стандартная неопределенность вычисляется по формуле:
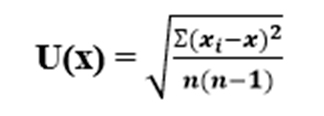
Стандартная неопределенность типа В
Если оценка берется из свидетельства о поверки, или иной документации, то она представляет собой интервал +/- а входной величины от ее оценки.
Тогда расчет стандартной неопределенности прямо зависит от закона распределения:
- При равномерном распределении :
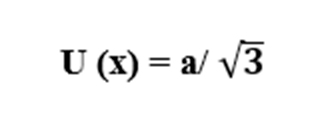
Где а – верхний интервал, в котором находится значение входной величины, т. К границы погрешности прибора симметричны.
- При треугольном распределении:
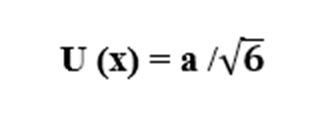
Суммарная стандартная неопределенность при некорреляционных входных величинах вычисляется по формуле :
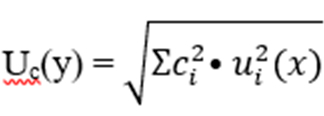
Где Сi – коэффициент чувствительности,
Ui(x) – стандартная неопределенность каждой входной величины
Расширенная неопределенность определяется путем умножения суммарной стандартной неопределенности на коэффициент охвата k (пример: на уровне доверия 95% k=2) :
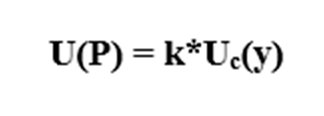
Полный результат измерения в конечном итоге записывается как:
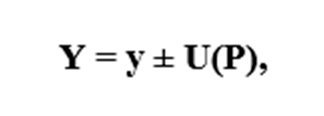
Где y – оценка измеренной величины Y
U(P) – расширенная неопределенность
Таким образом расчет неопределенности измерения не только в более широком плане позволяет проследить и оценить разброс значений измерения, но и позволяет претендовать на международное признание деятельности калибровочных и испытательных лабораторий, так как расчет неопределенности измерения является одним из требований ISO IEC 17025.
После чего стандартная неопределенность вычисляется по формуле:
Стандартная неопределенность типа В